隨著齒輪結構的優化改進,弧齒錐齒輪也被廣泛使用,因其具備高承載強度、穩定動力傳輸、使用壽命長的優勢,目前已在汽車機械動力系統等方面發揮了不可替代的作用。弧齒錐齒輪在使用階段最容易發生齒面磨損的現象,從而導致運行故障。當形成齒面磨損時,將會造成齒輪系統出現明顯振動、噪聲和無法滿足齒輪系統間精確傳動的技術要求,最終增大了傳動的誤差。
目前已有較多研究人員開展了直齒圓柱齒輪齒面的磨損因素分析,并探討了動態傳動誤差的變化情況。高洪波等從動態嚙合剛度、摩擦、齒側間隙、偏心等層面進行分析,為單級直齒圓柱齒輪傳動結構建立了 6 自由度的耦合模型,分別研究了全齒發生均勻與偏心磨損時的特征。結果顯示,逐漸提高齒面的磨損程度后,形成了均值與波動性更大的動態傳動誤差。王彥剛等針對含齒面磨損故障建立了二級齒輪箱傳動誤差分析模型,經測試表明,動態傳動誤差信號與傳統形式的齒輪箱振動響應信號相比可以獲得更大信噪比,并且可以更好地適應變速變載運行工況,提升了整體穩定性。此外,還可以根據動態傳動誤差準確識別復雜結構齒輪在初期階段發生齒面磨損情況。但是這些研究內容都是針對直齒圓柱齒輪的,對于復雜齒形結構的弧齒錐齒輪則沒有建立明確的傳動誤差分析方法,而且以上提出的齒輪動力學模型基本都是屬于集中參數模型,在實際建模階段無法完全確定齒輪系統參數,對最終精度造成較大影響,并且實際計算過程也過于復雜。
根據以上分析,本文對服役期間的弧齒錐齒輪齒面磨損進行了深入研究,針對各個載荷與磨損狀態下單齒和全齒磨損的齒輪構建了傳動誤差曲線,由此判斷載荷與磨損程度引起的弧齒錐齒輪動態傳動誤差變化情況。
1、齒面磨損模型
將傳動誤差理解為齒輪副在嚙合線方向上產生的相對位移 δ,表達式如下:
式中:Rp與 Rg分別為主動輪與從動輪半徑;θp、θg 分別為主、從動輪沿軸心線發生扭轉的自由度。
本文針對剛性支撐條件的弧齒錐齒輪構建了純扭振模型,以探討齒面磨損故障引起的齒輪系統傳動誤差變化情況。
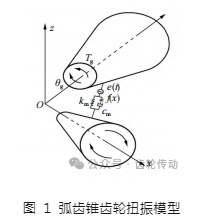
弧齒錐齒輪扭轉振動模型
圖 1 給出了弧齒錐齒輪扭振模型。以 x 軸與 y 軸表示主動輪與從動輪的軸心線位置,原點位于兩軸的交點處,構建得到 O-xyz 坐標系。進行仿真分析時,假定 2 個齒輪都位于理論坐標處,將齒輪軸視為一個沒有質量的剛體,通過質量與轉動慣量集中的形式實現對齒輪的模擬功能,由此獲得含有 2 個自由度的齒輪系統。根據齒輪系統的受力狀態建立以下弧齒錐齒輪副扭轉振動模型函數:
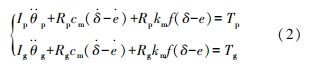
式中:Ip、Ig 分別表示主動輪與從動輪轉動慣量;Tp、Tg分別表示主動輪與從動輪驅動力矩與載荷產生的力矩;e 表示齒輪副靜態傳動誤差;cm表示齒輪副嚙合阻尼;km表示齒輪副時變嚙合剛度;f 是齒側間隙函數。
將兩弧齒錐齒輪嚙合點在振動與誤差作用下形成的嚙合點法線相對位移表示成以下形式:
上式合并后得到:
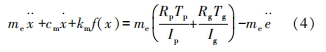
齒面磨損故障激勵機理
對式(3)進行分析可以發現,弧齒錐齒輪扭振微分計算方程跟常規動力學方程接近,可對 2 個式子進行對比分析。以下為典型動力學方程:
式中:M 表示質量矩陣;K 表示剛度矩陣;C 是阻尼矩陣;P 是載荷。
以上式建立的齒輪系統動力模型都涉及慣性力、彈簧力、阻尼力、載荷力的相互關系。但相對動力學基本方程存在明顯差異,齒輪在實際運動階段受到靜態傳動誤差、時變嚙合剛度、齒側間隙各類非線性作用條件的綜合影響,這使得齒輪系統形成了明顯的傳動誤差。產生齒面磨損故障時,將會引起齒輪系統的各項力學特性參數變化,在齒輪系統中形成了不同內部激勵,從而在齒輪系統中形成不同的動態傳動誤差。
對弧齒錐齒輪進行扭振模型計算過程較為復雜,需要耗費大量時間解析,因此通常都是選擇數值的方式完成求解過程。為了進化集中參數模型,優化了齒輪的關鍵參數,這對計算精度也造成一定的影響,只能利用非線性分析的方式研究齒輪的動力學特性。根據有限元實體模型進行處理時只需設置合適的幾何精度與邊界參數便可以獲得精確結果。
2、弧齒錐齒輪建模
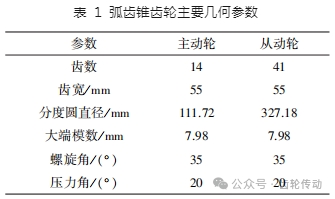
本文利用 Matlab 軟件完成齒面離散點的編程計算,再利用建模軟件對齒面實施擬合,由此構建得到弧齒錐齒輪模型,各項參數如表 1 所示。
齒面發生磨損的一個重要形式是輪齒厚度減小,因此本研究利用控制齒厚參數的方式來表示齒面的磨損狀態。齒輪運行期間,主動輪相對從動輪會發生更多的齒面接觸,在同樣的材料下,主動輪齒面會產生更大程度的磨損。因此本文以主動輪作為故障分析對象。通過調整輪齒齒厚參數模擬單齒、全齒發生齒面磨損情況,構建了齒面發生不同磨損程度時的仿真模型。
對材質為 45Cr 的弧齒錐齒輪開展動力學仿真測試,各參數如表 2 所示。
進行模型計算時加入了阻尼因素的作用,設置 Ray 阻尼,質量矩陣系數為 α = 0.03,剛度矩陣系數為 β = 3×10-6 ;齒輪副保持摩擦接觸狀態,對應的摩擦因數為 0.1;主動輪和從動輪都只沿軸心 線發生旋轉,保持主動輪轉速為 210 r/ min,控制從動輪轉矩依次為 500 Nm、1 000 Nm、3 000 Nm,再對齒輪進行傳動特性分析。
3、動態傳動誤差結果分析
通過仿真計算獲得主動輪和從動輪產生的轉動角大小,根據測試結果得到動態傳動誤差變化曲線。依次計算單齒與全齒磨損條件下形成的動態傳動誤差,最后對比了不同磨損程度下動態傳 遞誤差。
單齒磨損動態傳動誤差曲線
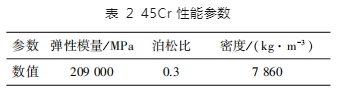
根據仿真得到的最初 0.13 s 的動態傳動誤差并繪制成相應的曲線,圖 2 給出了在載荷為 500 Nm 條件下各單齒磨損量形成的傳動誤差。
由圖 2 可以發現,在保持磨損量不變情況下,齒輪經過一個很短時間的瞬態狀態后開始轉為穩態階段。當磨損輪齒發生嚙合時,系統中產生了更明顯的激勵,從而形成了更高的動態傳動誤差 γ;時間增加至最值 Γ 時,嚙合狀態逐漸消失,引起動態傳動誤差 γ 的持續降低。通過分析圖中各顏色標注的曲線可以發現,在初始階段齒面發生磨損時,提高齒面磨損量 λ 時,動態傳動誤差 γ 也發生了上升的趨勢,同時獲得了更大的 Γ;弧齒錐齒輪具備較大重合度,隨著齒面磨損量 λ 超過臨界值后,磨損輪齒的載荷作用消失,此時位于磨損輪齒邊緣區域的輪齒可以對故障齒起到載荷分擔的效果,動態傳動誤差 γ 已經與此載荷臨界值 γ1一致。
在持續提高載荷 P 的過程中,輪齒形成了更大程度的彈性形變,保持同樣的磨損量時形成了更大的動態傳動誤差 γ,此時產生了更大的動態傳動誤差臨界值 γ1。由于在變形過程中可以發揮補償的效果,以降低了動態傳動誤差的波動性,能夠在更短時間內完成瞬態轉變,使整體變化更加平緩;從而形成了明顯滯后的動態傳動誤差最值 Γ。
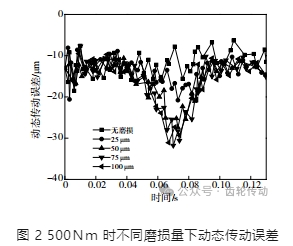
為分析 λ、P 引起的 Γ 變化,選擇 λ 作為自變量,以 Γ 作為因變量擬合得到圖 3 結果。分析圖 3可以得到以下結論。
1)恒定載荷下,發生初始階段的齒面磨損時, Γ 和 λ 表現為單調遞增的趨勢,提高齒面磨損量 λ 后,發生了擬合函數斜率 ε1突變達到 0,獲得上述載荷的誤差臨界值 γ1 。
2)提高載荷 P 后,擬合函數斜率 ε1和截距 η1 都形成了更大的絕對值;考慮到弧齒錐齒輪具備較高重合度,此時臨界值 γ1狀態發生持續提高。
全齒磨損動態傳動誤差曲線
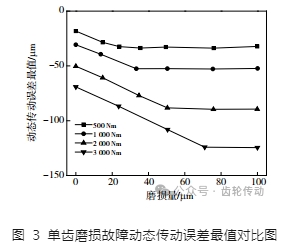
當發生全齒磨損故障時,對各載荷進行動態傳動誤差測試得到圖 4 結果。對圖 4 進行分析可以發現,逐漸提高齒面磨損量時,形成了更大的動態傳動誤差。當載荷提高后,曲線可以在更短時間內進入穩態階段,大幅減小了波動性,形成了更大的動態傳動誤差 γ 絕對值。
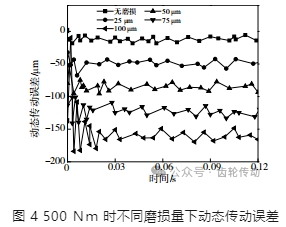
所有齒輪都達到相同的磨損量,不會出現單齒故障情況下磨損齒不受載荷作用的現象,這使得在全齒磨損故障條件下形成了更穩定的動態傳動誤差。
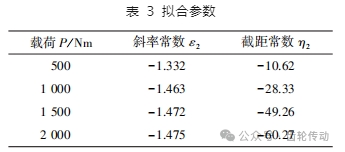
全齒磨損故障動態傳動誤差平均值對比結果如圖 5 所示。分析圖 5 發現,全齒磨損量 λ 和傳動誤差均值 E 形成了線性變化的特征,各載荷下形成了幾乎平行的擬合直線,得到表 3 的各項參數。
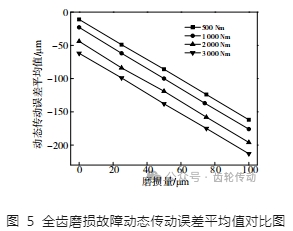
繼續擬合可得
利用式(6)可估算出存在全齒磨損故障條件下弧齒錐齒輪動態傳動誤差。
4、結語
1)提高齒面磨損量 λ 時,動態傳動誤差 γ 上升,獲得了更大的 Γ;處于恒定載荷下時,初始階段 Γ 和 λ 表現為單調遞增的趨勢;提高齒面磨損量 λ 后,擬合函數斜率突變達到 0。提高載荷 P 后,擬合函數斜率和截距都形成了更大的絕對值。
2)逐漸提高齒面磨損量時,形成了更大的動態傳動誤差。當載荷提高后,曲線可以在更短時間內進入穩態階段,大幅減小了波動性,形成了更大的動態傳動誤差 γ 絕對值。
參考文獻略.
